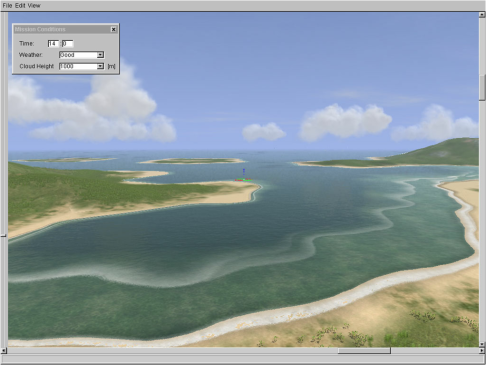
[1] published a complex water rendering approach, which was used in the game WWII:online as well. The presentation can be listened on-line here (in Russian). The bases of a their water shader is a general illumination equation, like the ones discussed in the Water mathematics chapter. Ambient light, diffuse light and also specular lights are taken into account. The Fresnel term is approximated with the cheapest method discussed in Alternative solutions: Simpler solution. The following screen-shot visualizes the result:
Optimizations
Using approximations and heuristics were applied in their water shader to get higher frame rates. They used the following general ideas:
- Using cheaper calculations instead of most accurate ones.
- Refreshing the reflection map only a few times in a second. (This can result artifacts when the movement is too fast.
- Optimizing shader code with different compilers.
These optimizations are needed to render real-time and visually convincing water surface. Although, the list contains general ideas only, they are useful for every computationally complex scene. The details of the approaches need to be adjusted to the required results.
Combining layers
To get a realistic result, several different technique is combined. There are areas of water and land, but the border between them is much more complex. There is a wavy area around the coast - waves are going towards the beach. Where the water is shallow caustics are also visible. Finally, there is a zone, where the waves run out over the sand.
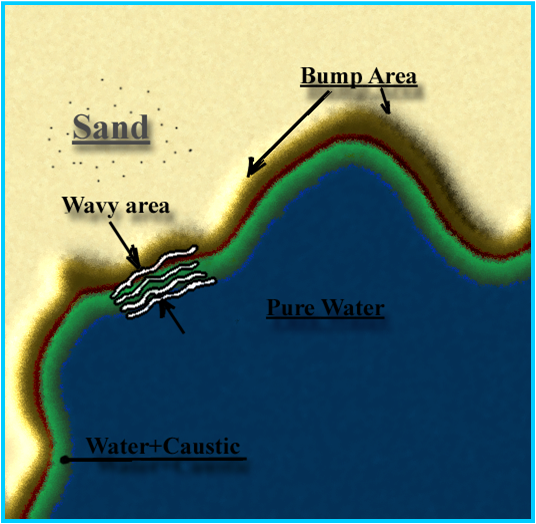
For a complex water-shader, the alternatives must be chosen after exhaustive consideration. The deepness of water, the viewing angles, the viewing distances and the length of waves are just some of the factors, which needs to be taken into account.
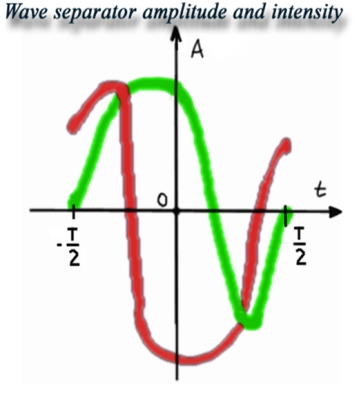
Coastal wave formation
In their approach complex mathematical equations are used to determine the wave formations. The waves need to go towards the beach, and their sinusoidal shape are displaced by functions depending on horizontal coordinates, time and on an extra variable which influences the shape like weather conditions. For more detailed explanations and mathematical background, see [KRI]. The next figure shows their wave-formation:
HLSL code
Their shader code differentiates the wave types. After the common variable declaration in the first part, they use 20 GPU instructions to calculate the reflections by a cube map, to compute the Fresnel term and the fog effect in the next section. They also use pre-generated normalvector-map to gain performance. The third part in their shader code calculates the appearance of high quality water. 55 instructions are needed to compute the permutation of the original texture coordinates, determine the normal vectors, weather conditions, and reflected color. Cloud shadow and foam texture is added to the result as well. The amount of foam is computed by a separate function. These parts are visualized on the next figures:
STARTUP PART
arbfp1 half4 main {
uniform half4 cc[6],
in half4 Col0 : COLOR0,
in half4 Col1 : COLOR1,
in float2 NVec : TEXCOORD0,
in float2 NVec1 : TEXCOORD1,
in float2 NVec2 : TEXCOORD3,
in float3 NCubM : TEXCOORD2,
in float3 EyeVec :TEXCOORD4,
in float4 ScrPrj :TEXCOORD5,
in float2 LMCrd :TEXCOORD6,
in float2 RMCrd :TEXCOORD7,
uniform sampler2D NMap,
uniform sampler2D NMap1,
uniform samplerCube NormCMap,
uniform sampler2D NMap2,
uniform samplerCube EnvCMap,
uniform sampler2D WRefl,
uniform sampler2D LMap,
uniform sampler2D RMap
} : COLOR
Fastest Water shader – 20 instructions using only cub map, Fresnel term and fog computation
{
fixed3 N = 2*tex2D(NMap1,NVec1).xyz-1;
fixed3 Eye = -texCUE(NormCMap, EyeVec.xyz).xyz * 0.5;
half dotEye_N = dot(Eye,N);
fixed3 reflectVec = 2*N*dotEye_N – Eye /**dot(N,N)*/;
half3 reflectColor = texCUBE(EnvCMap, reflectVec).xyz * 8;
fixed3 diffuseL = saturate(dot(N, c2.xyz));
fixed3 diffuse = diffuseL * c0.xyz;
half Fresnel = pow((1-max(dotEye_N,c3.b)),5)c3.g + c3.r;
half3 WaterColor = reflectColor*Fresnel+diffuse;
float RevFa = 1.0-Col0.a;
half4 Out; Out.xyz = WaterColor * RefFa + Col1.rgb;
Out.w = Fresnel * RevFa + col0.a;
return Out;
}
High quality water shader with 8 textures and 55 instructions
half Wavy = tex2D(RMap, RMCrd).w*c3.w; // 1 1.5, 0.5 0.75
fixed3 N0 = tex2D(NMap, NVec).xyz;
fixed3 N1 = tex2D(NMap1, NVec1).xyz;
fixed3 N2 = tex2D(NMap2, NVec2).xyz;
fixed3 N21 = lerp(N2,N1, c4.x);
half3 N = lerp(N21, N0, c4.y) – 0.5;
N.z *= Wavy; N = normalize(N);
half4 Scale_dsdt = half4(0.1*0.7,0.05*0.7,0.0,0.0);
half4 TexCrd = ScrPrj*pow(ScrPrj.w, -1.25);
TexCrd = TexCrd + Schale_dsdt * N.xyzz; // permutate original texture coordinates
fixed3 CloudsShadow = tex2D(LMap,LMCrd).xyz * c1.x + c1.y;
fixed3 PlaneRefl = tex2Dproj(WRefl, TexCrd).xyz;
half3 Eye = -texCUBE(NormCMap, EyeVec.xyz).xyz*0.5;
Eye = normalize(Eye);
half dotEye_N = dot (Eye, N);
half3 reflectVec = 2*N*dotEye_N – Eye /**dot(N,N*/;
half3 reflectColor = texCUBE(EnvCMap, reflectVec).xyz * 8;
fixed3 diffuseL = saturate(dot(N, c2.xyz));
fixed3 diffuse = diffuseL*c0.xyz;
reflectColor = lerp(reflectColor, PlaneRefl, c4.z);
half Fresnel = pow((1-max(dotEye_N, c3.b)), 5) * c3.g + c3.r;
refectColor * = Fresnel;
half3 WatercColor = reflectColor + diffuse;
half3 F3 = ((N21-0.5) * half3(3.15,3.15,0))/Wavy; half Foam = dot(F3, F3);
Foam = saturate(pow(Foam,4))*0.75;
half3 FoamColor = diffuseL*c5.xyz + c5.w;
WaterColor = lerp(WaterColor , FoamColor, Foam) * CloudsShadow;
float RevFa = (1.0-Col0.a);
half4 Out; Out.xyz = WaterColor*RevFa+Col1.rgb;
Out.w = Fresnel*RevFa+Col0.a;
return Out;
}
FOAM SHADER: 4 WAVES, WITH DRY COAST, 4 TEXTURES. 28 INSTRUCTIONS ALTOGETHER
half4 computeFoam (uniform sampler2D sCoast,
uniform sampler2D sFoam0,
uniform sampler2D sFoam1,
uniform sampler2D sSin,
uniform sampler2D sNoise,
uniform sampler2D Lmap
) : COLOR
{
fixex4 Coast = tex2D(sCoast, vCoast);
fixex4 Foam0 = tex2D(sFoam0, vFoam0);
fixex4 Foam1 = tex2D(sFoam1, vFoam1);
fixex4 SinA01 = tex2D(sSin, vSin);
fixex4 SinB01 = tex2D(ssin, vsinB);
half4 FoamC = Foam1;
fixed4 Dissolve = SinA01.zwzw; Dissolve.zw = SinB01.zw;
fixed4 SinA = SinA01; SinaA.zw = SinB01.xy;
fixed dA = Coast.a + c4.y + FoamC.r +0.5;
half4 A = SinA*c4.x+dA;
fixed SeaFactor = Col0.g ; Dissolve*=SeaFactor;
A = saturate(A*c0+c1)*saturate(A*c2+c3);
half4 Lighting = c4.z;
Lighting.a = saturate(dot(A,Dissolve));
FoamC = Lighting;
half4 T = FoamC.aaaa; T.a = -1;
FoamC = FoamC*T + half4(0,0,0,1);
//Fog
FoamC.rgb = FoamC.rgb*Col1.r+Col1.rgb*(1-FoamC.a);
return FoamC;
}









